数学的なパズルの工作室 "たためる 多面体"　--->　たためる多面体 の紹介

　　さて、正十二面体を書けますか？ 多面体について中学１年の数学で学んだとき、その実物模型に触ってみましたか？

　辺だけからなる多面体（多面体エッジグラフといいます）を作ると、変形可能なものができます。　図形変形は数学的に
大切な事柄ですが模型を作るには困難なことがあります。　　辺を細い材料で作ると立体図形なのに自立できないほど
ひ弱なものになります。　太い材料で辺を作ると平面状にたたむことはできません。　　そこで薄く丈夫なプラスチック板
をやや幅広く使って辺の材料とすることにします。　　それにより自立する強さと平らにたためることの両立が可能です。
欠点は、本来は直線のはずの辺が弓なりになること、頂点が尖っていないことなどです。　　　　　　　　　　　　　　　　　.

１）　材料

　Ａはプラスチック板を打ち抜いた部材で、長さ９８ミリ 巾１９ミリ 厚さ０．７５〜０．８ミリです。 Ｂは２つの部品をあわせる
タイプのハトメで、この２種類が使用する材料です。　　ハトメの打ち方は手加減が難しく、硬くとめると図形の変形ができ
ません、弱くとめるとハトメが外れてしまうことがあります。 ＢをＣのように前もって加工しておけば部材を差し込むだけで
すみます。　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　.

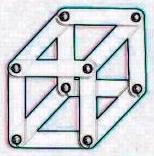
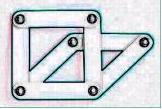
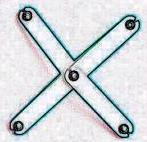
２）　立方体
　部材１２枚、ハトメ 8個で作ります、　頂点にあたるところで３枚重ねてハトメでとめます。
立方体というにはやや丸すぎますが、平面にたたむと、立方体の投影図にすることができます。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　.

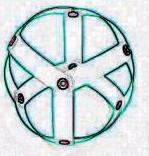
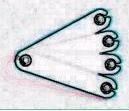
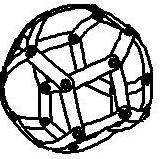
３）　正十二面体
部材３０枚、ハトメ２０個で作ります、　　　　　右３つの変形は難しいです。

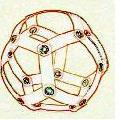
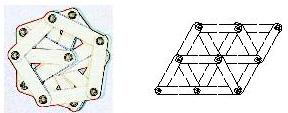
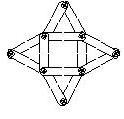
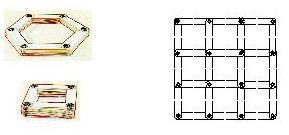
４）　十四面体（切頭正八面体）　部材３６枚、ハトメ２４個で作ります。
正八面体の頂点を切った形です、変化が多く楽しめる多面体です、正方形１つにたたむことは難しいです。
　　　　　

５）　その他
　三角形の面のある多面体は変形が無理であると考えるのが自然ですが、
三角形の面がいくつかあっても面白い変形が可能なものがあります。　 .

頑張って挑戦して頂いた人が自分のHPに掲載されております、ご苦労さまです。
たためる立体の変形の実際